kaksha.dev

---

Bits & Bytes

Computers store numbers in binary format. For example, the number 351₁₀ is represented as 0000000101011111₂. This is because, at their core, computers are electronic devices. It’s simpler to represent the binary output of electronic circuits, where the presence of electricity in a wire signifies “true” and its absence signifies “false.”

Electronic implementation

The diagram below illustrates that a wire with a voltage between 0 and 0.5 volts is interpreted as a 0, whereas a voltage around 5 volts is read as a 1. This range is designed to accommodate potential noise and inaccuracies in the wiring.

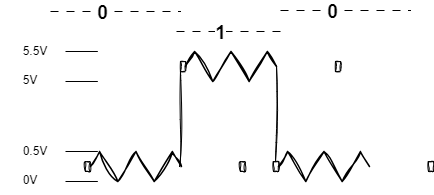
Encoding Byte Values

Binary

Byte = 8 bits (binary digits)
Example: 00101011₂ = 32+8+2+1 (0X2⁷+0X2⁶+1X2⁵+0X2⁴+1X2³+0X2²+1X2¹+1X2⁰) = 43₁₀
Example: 26₁₀ = 16+8+2 = 00101010₂

Hexadecimal

Hexadecimal is a base-16 numbering system where 1 byte is represented by 2 hexadecimal digits. It uses the digits 0 to 9 and the letters A to F (with A representing 10 and F representing 15). In C, hexadecimal numbers are prefixed with 0x, so FA1D37B₁₆ should be written as 0xFA1D37B or 0xfa1d37b.

Hex	Decimal	Binary	|	Hex	Decimal	Binary
0	0	0000	|	8	8	1000
1	1	0001	|	9	9	1001
2	2	0010	|	A	10	1010
3	3	0011	|	B	11	1011
4	4	0100	|	C	12	1100
5	5	0101	|	D	13	1101
6	6	0110	|	E	14	1110
7	7	0111	|	F	15	1111

Signed Integers : Negative Number Representation

Use the high order bit to indicate negative: call it the “sign bit”. Ex:
0x00 = 00000000₂ is non-negative, because the sign bit is 0
0x7F = 01111111₂ is non-negative
0x85 = 10000101₂ is negative

How to represent a negative number. One approach could be, just keep 1 at MSB. As illustrated in below image:

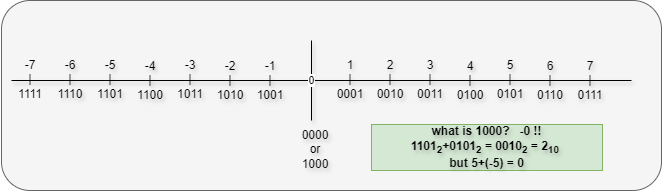As we can see, 4₁₀=0100₂ and hence -4₁₀=1100₂ But this approach is failing basic arithmatic operations like 4-4=0 and also 0000=0 and 1000 is -0. There is nothing like -0.

2’s Complement:
It can be calculated by adding 1 to 1’s complement. 1’s complement is flipping all the bits (~ operator) So, -n = ~n + 1 Benefits of using 2’s complement for negative numbers.

• It supports arithematic operations. 5₁₀=0101₂ and -5₁₀=1011₂ so, 5-5 -> 0101+1011=0000=0₁₀
• It is symmetric ie negative of nagetive 5 is positive 5. Also, 2’s complement of 2’s complement of 5 is 5.
• There is no confusion of -0 nad +0. 0 is 0000 while 1000 is -8

Boolean Algebra

• Algebraic representation of logic: Encode “True” as 1 and “False” as 0
• AND (&) : A&B = 1 when both A is 1 and B is 1. Can be used for padding. Ex: last 4 bits of an integer can be extracted using number & 1111.
• OR (|) : A|B = 1 when either or both A and B are 1.
• XOR (^) : A^B = 1 when either A or B is 1 but not both. Interestig property : A^0=A and A^A=0 hence XOR can be used to find lonely number in an array where other numbers are in pairs.

  int findLonelyNumber(int[] a){
    int result = 0;
    for(int t : a){
        result ^= t;
    }
    return result;
  }
  

  interestingly, when guest says she wants tea or coffee, she does not mean host to bring both. Actually, she meant “I want tea xor coffee”.

• NOT (!) : turns true to false and false to true. In case of numbers, 0 if non zero number, 1 when number is 0.
• TILDE (~) One’s Complement: flips all the bits of a variable. 1 to 0 and 0 to 1.
• LEFT SHIFT («) : Shift bit-vector x left by y positions. Throw away extra bits on left and Fill with 0’s on right. Equivalent to multiplying by 2^y
  x = 00000110(+3) then x « 3 = 00110000
  x = 11111010(-3) then x « 3 = 11010000
• RIGHT SHIFT (») : Shift bit-vector x right by y positions throw away extra bits on right Fill with 0s on left. Equivalent to dividing by 2^y
  x = 00000110(+3) then x » 2 = 00000001 (Replicate o’s on left)
  x = 11111010(-3) then x » 2 = 11111110 (Replicate o’s on left)
  Note: Replicate most significant bit on left Maintains sign of x. Logically, this is correct too. -10/2=-5 not some positive number.

Float Representation

A float has 3 part when stored by computer. sign, exponent and factor which can be interpreted as (sign)1XFX2^E-127 In 4 byte float, MSB is sign bit followed with 8 bits of Exponent and remaining 23 bits of Factor.
ex: 11000001001100000000000000000000 = -1 X 1.375 X 2 ^129-127 = 5.5
Note: factor is calculated by : 1 + 0X1/2 + 1X1/4 + 1X1/8

Excercise